|
|
|
 ε-δ를 이용한 극한의 엄밀한 정의 ε-δ를 이용한 극한의 엄밀한 정의
Mathematics |
2010. 4. 22. 20:10
|
|
|
(수정 중)
precise limits of function as x approaches a constant
The following problems require the use of the precise ε,δ definition of limits of functions as x approaches a constant. Most problems are average.
We will begin with the precise ε,δ definition of the limit of a function as x approaches a constant.
DEFINITION: The statement =L) has the following precise definition. Given any real number ε>0, there exitst another real number δ>0 so that has the following precise definition. Given any real number ε>0, there exitst another real number δ>0 so that
if  , \then , \then-L \mid <\varepsilon)
In general, the value of δ will depend on the value of ε. That is, we will always begin with ε>0 and then determine an appropriate corresponding value for δ>0. There are many values of δ which work. Once you find a value that work, all smaller values of δ also work.
To try and understand the meaning behind this abstract definition, see the given diagram below.
We first pick an ε band around the number L on the y-axis. We then determine a δ band around the nuber a on the x-axis so that for all x-values (excluding x=a) inside the δ band, the corresponding y-values lie inside the ε band. In other words, we first pick a prescribed closeness (ε) to L. Then we get close enough (δ) to a so that all the corresponding y-values fall inside the ε band. If a δ>0 can be found for each value of ε>0, then we have proven that L is the correct limit. If there is a singel ε>0 for which this process fails, then the limit L has been incorrectly computed, or the limit does not exist.
 는 는  를 포함하는 어떤 개구간( 를 포함하는 어떤 개구간( 는 제외될 수 있음)에서 정의된 함수라고 하자. 는 제외될 수 있음)에서 정의된 함수라고 하자.
만약 임의의 양수  에 대하여 에 대하여  일 때마다 일 때마다 -L \mid <\varepsilon) 을 만족하는 을 만족하는 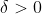 이 존재하면, 이 존재하면, 가 가  에 가까이 접근할 때 의 극한이 에 가까이 접근할 때 의 극한이  이라 정의한다. 이라 정의한다.
|
|
|
|
|
|
|
| wir mussen wissen, wir werden wissen! |
« 2025/05 »
| 일 |
월 |
화 |
수 |
목 |
금 |
토 |
| |
|
|
|
1 |
2 |
3 |
| 4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 11 |
12 |
13 |
14 |
15 |
16 |
17 |
| 18 |
19 |
20 |
21 |
22 |
23 |
24 |
| 25 |
26 |
27 |
28 |
29 |
30 |
31 |
|
|
Total :
Today :
Yesterday : |
|
|