Q) 
이 자연수일 때, 
이 소수이면,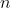 
도 소수임을 증명하라.
sol
이 소수이면 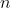도 소수이지만, 소수란 1과 그 자신이외에 약수를 갖지 않는 정수이므로,
(2^{n-1}+2^{n-2}+ \cdots +1))
에 의하여
(2+1))
-소수
(2^2+2+1))
-소수
(2^2+1))
-소수가 아니다.
에 구체적인 값을 대입한 결과, 위의 경우 이 소수가 아니면 도 소수가 아닌 것을 잠정적으로 알 수 있다.
여기서 대우를 증명해보자.
이 소수가 아니면, 
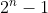도 소수가 아님을 증명한다.
(p,q는 모두 1이 아닌 자연수)라 하면,
p,q는 1이 아닌 자연수이므로
}+2^{p(q-2)}+\cdots+2^p+1)
은 자연수이고
특히, 
따라서 은 1과 그 자신 이외의 약수를 가지므로 소수가 아니다.
본 명제의 대우가 참임이 증명되었으므로, 본 명제도 참임이 증명되었다.
