함수
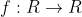
의 이계도함수
)
가 구간 [0,1]에서 존재하고 유계이다.
모든 자연수 n에 대하여
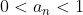
인 수열
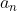
에 대하여 무한급수
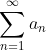
은 발산하지만,
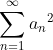
은 수렴한다.
무한급수
})
이 수렴하면, 무한급수
 \right|)
도 수렴함을 보여라.
(sum때문에 배열이 이상합니다.)
테일러와 연관이 깊은건 아니지만, 아는게 테일러뿐이라..
우선 문제를 풀기 전
)
가 폐구간 [a,b]에서 연속이고 개구간 (a,b)에서 미분가능할 때,
=f(a)+(b-a)f'(a)+\frac{(b-a)^2}{2!}f''(c))
임은 Role, Cauchy theorem 으로 알수 있다.
마찬가지로
=f(a)+(b-a)f'(a)+\frac{(b-a)^2}{2!}f''(a)+\frac{(b-a)^3}{3!}f'''(c))
이다.
 \sum{a_n}^2)
converges
)
converges
)
수렴
 f'(0)\sum a_n = \sum f(a_n)-\frac{{a_n}^2}{2!}\sumf''(c_n))
인데, 좌변에서
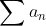
이 발산이고 우변이 수렴하기 때문에
|)
은 수렴한다.
Mathematics 에 해당하는 글39 개
