오랫만에 피보나치
= F_{gcd(m,n)})
)
Sol)
lemma1.
i) n=1 or 2
 성립
성립
 성립
성립
ii) n=k 일 때 성립한다면
+(F_{_m-1}F_{_n-2}+F_mF_{_n-1}))
n=k+1 일 때 성립

i) m=1
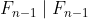 성립
성립
ii) m=k 일 때 성립한다면
귀납가설에 의해 ) 라 하면 lemma1. 에 의해
라 하면 lemma1. 에 의해
n-1}=F_{_mn+n-1}=F_{_mn-1}F_{_n-2}+F_{_mn}F_{_n-1} \\= F_{_n-1}(kF_{_n-2}+F_{_mn}))
=1) 이므로 수학적 귀납법에 의해 증명 되었다.
이므로 수학적 귀납법에 의해 증명 되었다.
\ gcd(F_{_m-1},F_{_p-1})=F_{_d-1}) 임을 보여도 된다. (단
임을 보여도 된다. (단 ) )
)
=k) 라 하자.
라 하자.
i) 임을 보이자.
임을 보이자.
lemma2. 에 의해  (단, m=dx), 또
(단, m=dx), 또  (단 p=dy)
(단 p=dy)
따라서 
ii)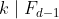 임을 보이자.
임을 보이자.
d=mx-py를 만족하는 x,y가 존재하므로 lemma1.에 의해
그런데 lemma3.에 의해
=1) 이므로
이므로 =1) 이다.
이다.
따라서 
i)과 ii)에 의해  이다.
이다.