Carrot이 학교 행사로 무지 바쁠 때 내준 문제. 늦게 풀어 미안함.
문제를 살펴 보자.
At what point on the ground does a perpendicularly suspended rod appear largest?
어느 지점에서 수직으로 매달린 막대기가 가장 크게 보이겠는가?
풀고보니(대수로) 유명한 레기오몬타누스의 최대각 문제
P점을 시점으로 잡고 PB와 지면이 이루는 각을  라 하고 PA와 지면이 이루는 각을
라 하고 PA와 지면이 이루는 각을 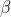 라 하자.
라 하자.
그렇다면 시야각 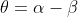 가 된다.
가 된다.
그리고 막대기에서 수직으로 내린 점과 P점 사이의 거리를 X라 하자.
이때, 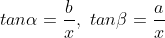 가 된다.
가 된다.
앞의 것을 대입하면 }=\frac{\frac{b}{x}-\frac{a}{x}}{1+\frac{b}{x}\frac{a}{x}}=(b-a)\frac{x}{x^2+ab})
시야각의 최대값을 찾기 위해 미분을 해보자.
\frac{x}{x^2+ab} \right)=(b-a)\frac{ab-x^2}{(x^2+ab)^2}) (단, x는 거리이므로
(단, x는 거리이므로 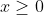 )
)
극대, 극소를 따지면 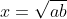 에서 극댓값을 갖는다.
에서 극댓값을 갖는다.
따라서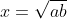 지점에서 막대기가 가장 크게 보인다.
지점에서 막대기가 가장 크게 보인다.
cf) 굳이 미분하지 않고 분자, 분모를 뒤집어 산술기하를 써서 최솟값을 찾아도 가능.
A,B,P를 지나는 원을 그린다.
) 임을 알 수 있다.
임을 알 수 있다.
즉 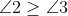 라는 말이다.
라는 말이다.
다시 말해, 원 바깥의 수평선 상에 어떤 점을 잡아도 원과 접한 부분의 각보다 크지 않다는 것이다.
그림에서 ^2=OA \cdot OB) 이므로
이므로 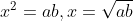 에서 최대가 된다.
에서 최대가 된다.
그림 출처 wikidot